C-spin RESEARCH Themes
Heusler Database
Explore Heusler Alloys
The database, developed by William Butler's group at the University of Alabama and Prof. Avik Ghosh's group at the University of Virginia, provides information on three families of Heusler alloys, “full” Heuslers (A2BC), “half” Heuslers (ABC) and “inverse” Heuslers (ABAC). For each of these families, calculations for numerous systems are provided: 180 for full Heuslers, 378 for half Heuslers and 405 for inverse Heuslers. For each system, the calculated minimum energy, lattice constant, magnetic moment, density of electronic states and formation energy are provided. You can even search for specific materials. They have also provided information about the stability of these phases relative to possible competing phases by linking to the OQMD database of calculated alloy phases. For each alloy, there is also a (probably incomplete) bibliography of experimental records.
What's in the database?
We calculated the electronic and magnetic properties of 180 full, 378 half and 408 inverse Heusler alloys using density-functional theory (DFT). Element selected for A, B and C atoms are listed below.
| Full Heusler | Half Heusler | Inverse Heusler |
| A – Cr, Mn, Fe and Co | A – Cr, Mn, Fe, Ru, Co, Rh and Ni | A – Cu, Ni, Co, Fe, Mn, Cr, V, Ti and Sc |
| B – Ti, V, Cr, Mn and Fe | B – Ti, V, Cr, Mn, Fe and Ni | B – Zn, Cu, Ni, Co, Fe, Mn, Cr, V and Ti |
| C – Al, Ga, In, Si, Ge, Sn, P, As and Sb | C - Al, Ga, In, Si, Ge, Sn, P, As and Sb | C - Al, Ga, In, Si, Ge, Sn, P, As and Sb |
Details About DFT Calculations
The calculations were performed using the Vienna Ab-Initio Simulation Package (VASP) which uses a plane wave basis set and projector-augmented wave (PAW) based pseudo-potentials. A uniform cut-off energy of 520eV was chosen for all calculations. The Perdew-Burke-Ernzerhof (PBE) version of the generalized gradient approximation (GGA) to the exchange correlation functional of DFT was adopted. The pseudo-potential version for each element is listed below. These pseudo-potentials were chosen to be consistent with those used to construct the OQMD database of calculated energies of alloy phases.
| Zn: PAW_PBE Zn 06Sep2000 1 | |
| Cu: PAW_PBE Cu 05Jan200 | |
| Ni: PAW_PBE Ni 06Sep2000 | Al: PAW_PBE Al 04Jan2001 |
| Co: PAW_PBE Co 06Sep2000 | Ga: PAW_PBE Ga_d 06Sep2000 |
| Fe: PAW_PBE Fe 06Sep2000 | In: PAW_PBE In_d 06Sep2000 |
| Mn: PAW_PBE Mn 06Sep2000 | Si: PAW_PBE Si 05Jan2001 |
| Cr: PAW_PBE Cr 06Sep2000 | Ge: PAW_PBE Ge_d 06Sep2000 |
| V: PAW_PBE V 08Apr2002 | Sn: PAW_PBE Sn_d 06Sep2000 |
| Ti: PAW_PBE Ti 08Apr2002 | P: PAW_PBE P 17Jan2003 |
| Sc: PAW_PBE Sc_sv 07Sep2000 | As: PAW_PBE As 06Sep2000 |
| Ru: PAW_PBE Ru 06Sep2000 | Sb: PAW_PBE Sb 06Sep2000 |
| Rh: PAW_PBE Rh 06Sep2000 |
The integration over the irreducible part of the Brillouin zone was done using the “automatic” 50 Monkhorst-Pack k-point grid and linear tetrahedron method with Blöchl corrections . The superlattices were relaxed without any constraint on shape or volume, using the conjugate-gradient algorithm. When ionic relaxations were performed, the stopping-criterion for structural optimization was an energy change less than 10-5 eV.
Determination of Lattice Constants
For a given A, B and C combination, we performed full ionic relaxations within a tetragonal cell for all of the Heusler alloys. Some of these alloys were found to remain in the cubic L21, C1b and XA structures, while some relaxed to a tetragonal structure; i.e. c/a is not equal to 1. Some of the half Heusler alloys were neither cubic nor tetragonal. All relaxations started from the cubic structure with small displacements to avoid vanishing of the net force on each atom due to symmetry.
Heusler alloys are prone to having multiple DFT solutions with different magnetic configurations. Therefore all energy versus lattice constant calculations were performed using multiple initial magnetic moment configurations, no moment, parallel moments and anti-parallel moments of the transition metal atoms.
The ground state of the Heusler alloy was determined by analyzing the results of the relaxation and cubic studies. For CoMnAl (Fig. 1), the Heusler alloy is stable when its lattice constants is 5.46 Å and the magnetic configuration of the A and B atoms is ferrimagnetic.
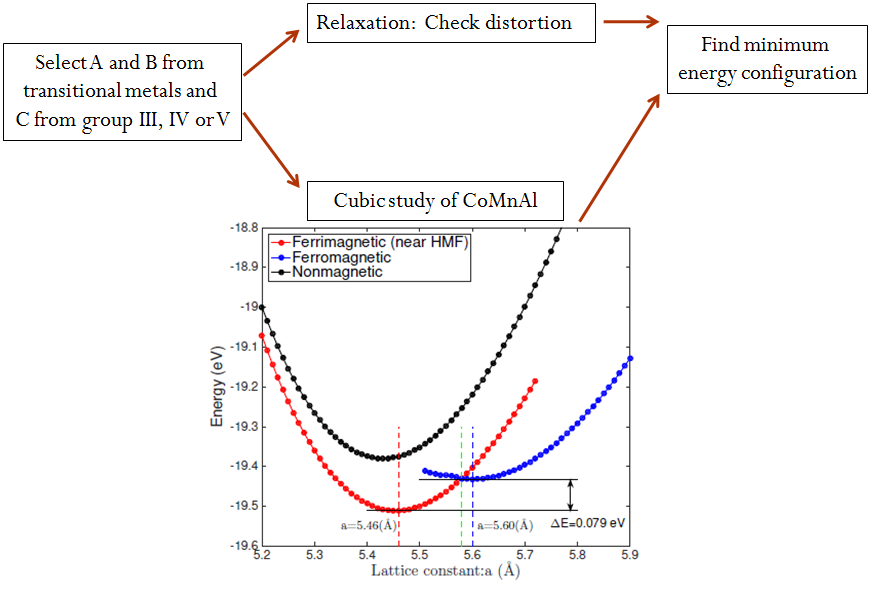Figure 1Formation Energy Per Atom
The formation energy per atom for each of the Heusler alloys was calculated by subtracting the energies of the individual elements in pure form from the alloy's total energy. For full Heusler A2BC, the formation energy per atoms is:
where EA2BC is the total energy of the full Heusler unit cell containing 4 atoms (two A, one B, one C), EA, EB and EC stand for the energies when A, B, C, X, Y and Z elements crystallize in pure metals, respectively. If the formation energy per atoms is positive, the alloy is unstable and cannot be formed in equilibrium conditions. Negative formation energy per atom suggests that such an alloy may be grown. However, negative formation energy does not, for example, guarantee against formation of binary or ternary phases comprising any two or three of the available three elements. The reference states for the elements were chosen to be consistent with the OQMD database so that formation energies in this database can be compared to those of competing phases in the OQMD database.
Using the database
The Heusler database includes calculations on almost 1,000 materials, including formation energy, stability and magnetic moment.
To begin a search, select an A element, B element and C element, or any combination thereof. Note that not every column must have a selection. For example, a selection of Ti for the B element will display every material in the database which has titanium in the B position, as pictured below.
Additional filters are provided in the Choices box. The function of each is described below.
| Full Heusler | Displays only materials with the full Heusler A2BC structure |
| Half Heusler | Displays only materials with the half Heusler ABC structure |
| Inverse Heusler | Displays only materials with the inverse Heusler ABAC structure |
| Stable | Displays only materials which are stable (have a negative formation energy) |
| Show All | Displays every material in the database. Please note that this option may take several moments to load |
| Clear | Clears the current search and resets the search table |
To select a material, simply click its name (written in red) in the results table.
Using the OQMD interface
Once a material has been selected, its information will be displayed. Every material in the database will display the OQMD interface option. Clicking on the OQMD interface title will toggle the interface. To display the OQMD website in its own tab, select the pop-out icon.
Enter the material in question into the search box within the OQMD interface and select submit. This will display a table of phases and formation energies (you may need to scroll down to view it). As of now, the OQMD website does not allow new phases to be entered to for GCLP calculations. We recommend replacing the highest positive formation energy found in the OQMD table with the value found in the Heusler database. Enter the phase and new formation energy found in the Heusler database and select re-evaluate to see updated information. For further information, consult the OQMD documentation.
If you have any questions or technical issues to report, please contact the database creators at: heuslerdatabase (AT) gmail (DOT) com
